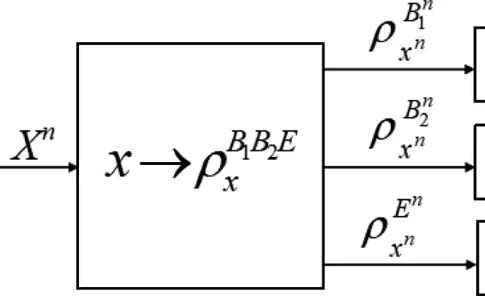
В недавнем исследовании, посвящённому теории квантовой информации, учёные представили подробный анализ приватного классического предела ёмкости канала классическо‑квантового вещания, обслуживающего сразу три получателя. Об этом сообщает link.springer.com.
Основой работы стал строгий математический аппарат, построенный на свойствах типичных и условно типичных подпространств, который позволяет оценить вероятность ошибок при передаче информации через такой сложный канал.
В начале доказательства авторы вводят понятие типичного подпространства. Рассматривается оператор плотности ρ, разложенный по собственным векторам |x⟩ с соответствующими собственными значениями p(x). Эти значения образуют закон распределения вероятностей: они неотрицательны и в сумме дают единицу, а их энтропия совпадает с вон‑Ноймановой энтропией S(ρ). Для δ‑типичной последовательности x₁,…,xₙ выполняется неравенство, связывающее среднее логарифмическое произведение вероятностей с энтропией, что полностью соответствует классическому определению типичности.
Типичное подпространство T_{ρ,δ}^{Aⁿ} определяется как линейная оболочка всех векторных произведений |x₁⟩⊗…⊗|xₙ⟩, где последовательность xⁿ принадлежит множеству δ‑типичных последовательностей Xⁿ. На это подпространство проецирует оператор Π_{ρ,δ}^{Aⁿ}, представляющий собой сумму проекторов на каждое из типичных состояний. Такое построение позволяет изолировать большую часть вероятностной массы в небольшом подпространстве, что является ключевым шагом в оценке ёмкости канала.
Далее вводится условно типичное подпространство, зависящее от фиксированной последовательности xⁿ. Для каждого xⁿ рассматривается ансамбль состояний ρ_{xⁿ}^{Aⁿ} с собственным разложением по векторам |y_{xⁿ}ⁿ⟩ и условным распределением p_{Yⁿ|Xⁿ}(yⁿ|xⁿ). Условно типичное подпространство T_{ρ,δ}^{Aⁿ|xⁿ} состоит из всех векторов, соответствующих условно типичным последовательностям yⁿ, а соответствующий проектор Π_{ρ,δ}^{Aⁿ|xⁿ} суммирует проекции на эти векторы. Эти конструкции позволяют учитывать зависимость между входными и выходными данными канала, что особенно важно при наличии нескольких получателей.
С помощью типичных и условно типичных подпространств авторы выводят границы ожидаемой средней вероятности ошибки при передаче классической информации через квантовый вещательный канал. Полученные оценки показывают, что при правильном выборе кодов и декодеров можно достичь приватного классического предела, при котором информация остаётся защищённой от посторонних наблюдателей, а каждый из трёх получателей способен восстановить свою часть сообщения с произвольно малой ошибкой.
Результаты исследования открывают новые возможности для разработки защищённых квантовых сетей связи, где одновременно обслуживаются несколько конечных точек. Практическая реализация таких каналов может стать фундаментом для будущих систем распределённой квантовой криптографии и многопользовательских квантовых коммуникаций, обеспечивая высокий уровень надёжности и конфиденциальности передаваемых данных.